Large ensemble simulations for the study of extreme hydrological events
Contributed by Karin van der Wiel, KNMI*.
The investigation of extreme hydrological events is often limited by the length of observed records or model simulations. For this reason many statistical extrapolation methods have been developed. In a recent GRL paper we advocate a novel method for the study of extreme events, which does not rely on such extrapolations (Van der Wiel et al., 2019).
In this blog post I invite you to take a slight step outside the HEPEX world – I will not discuss hydrological ensemble prediction. Instead, I will discuss the use of large ensemble simulations for scientific research of extreme hydrological events. Specific research topics that may benefit from large ensemble simulations are, for example, the investigation of the severity or occurrence of extreme events, a study of the physical processes leading to extreme events, or the making of projections of the effects of global climate change on extreme events.
Extreme event analysis
In essence, there are two methods for the investigation of extreme events:
- by means of a statistical model of the tail of the distribution of events, or
- by means of sampling, based on a long time series.
Observational time series are generally short, especially compared to the return period of the extreme events that societies want to prepare for. Therefore, we often use a statistical extrapolation method to investigate these extreme events. It is assumed that extreme events follow a single probability distribution, often GEV based, and that information of observed extremes (e.g. return period ~10 years) can be extrapolated to non-observed extremes (e.g. return period >100 years).
There are cases, as we will see later, where these assumptions fail. In such cases the statistical method cannot be used because it could lead to significant over- or underestimation of the magnitude of extreme events. In hydrology this may occur in river basins where multiple runoff generating processes can lead to extreme events (e.g. overland flow, rain-on-snow events or extreme rapid snowmelt). If the scientist or engineer is aware of this or this behaviour is captured by the data, she will note that the statistical method is unreliable and won’t use it for further study. However, given limited data, there is a danger we miss the double distribution, which could lead to an underestimation of the risks of hydrological extremes.
If we use the second method, sampling of extreme events, we are not at risk of such errors. Unfortunately, the length of time series often limits the use of this approach as it is not possible to investigate unobserved events. In theory, model experiments can be of unlimited length, and recent developments in computing power now also allow such very long time series or large ensembles to be created. Empirical studies based on sampling of extreme events, instead of statistical studies, will therefore likely become more common in the near-future.
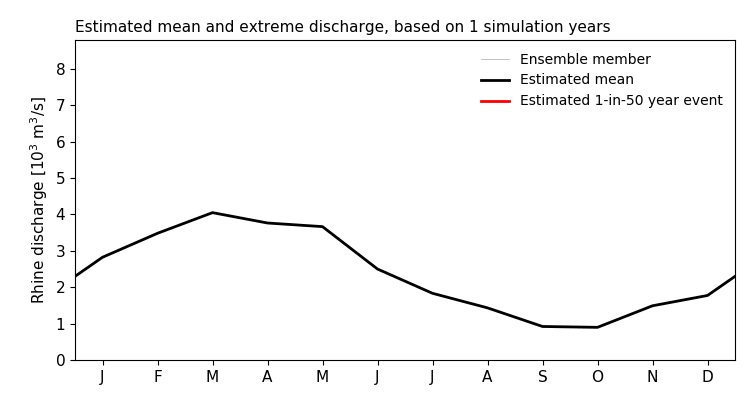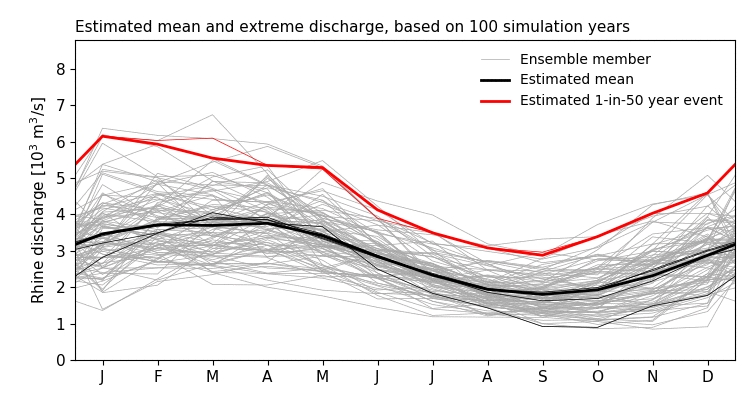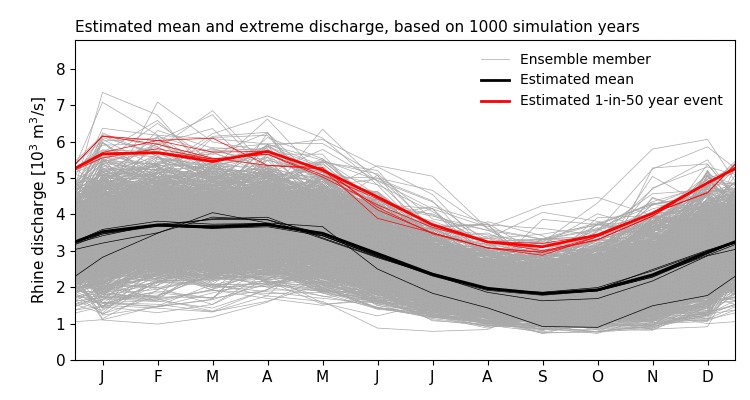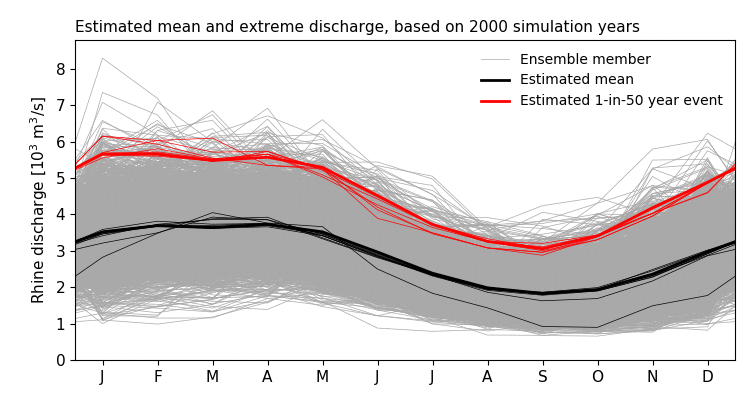
Figure 1: Example of extreme event analysis (1-in-50 year return period, red lines) by means of sampling. Estimates from different ensemble sizes are shown.
When statistical extrapolation fails
I will now present a case study from the paper for floods in the Amazon River, to show what could go wrong if one relies on statistical extrapolation (Figure 2). Based on a large ensemble hydrology simulation (2x 2000 years) using the global hydrological model, PCR-GLOBWB 2, we compared the statistical method to the sampling method.
First, a GEV analysis based on 100 years of simulated discharge data. The GEV-fit describes the data in the subsample well, and matches observed discharge relatively okay. Based on this information alone, we might feel confident in using these data for extrapolations to the 1-in-200 year flood. However, when we include the full 2000 years of simulated discharge data it becomes obvious that the GEV-fits fail to describe the most extreme floods (unobserved in the 100-year subsample). In this model there is a clear double distribution. With this information, no-one would rely on GEV statistics to estimate the 1-in-200 year flood.
Instead, we can use the information in the full distribution to sample 200-year floods. This sample can be used to estimate typical discharge levels during such events (as in Figure 2), but can also be used to find the meteorological and hydrological processes that lead to these events.
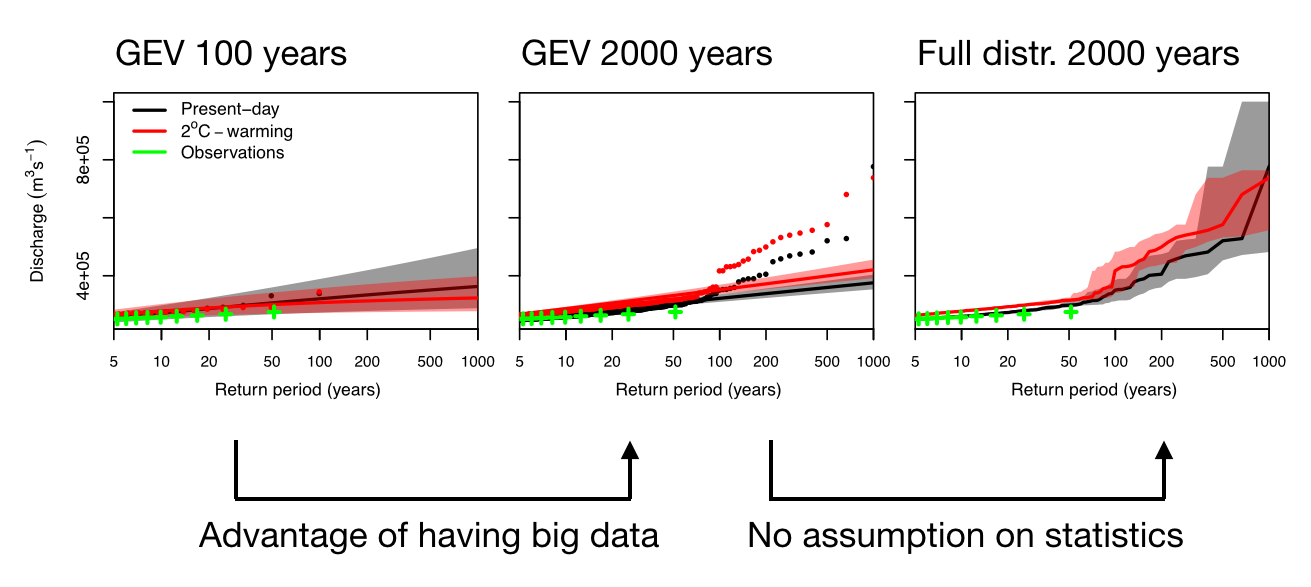
Figure 2: Analysis of extreme high discharge in the Amazon River. Left: GEV-fits based on 100 years of data. Middle: GEV-fits based on 2000 years of data. Right: Empirical distribution estimate based on sampling of 2000 years of data. Figure adapted from Van der Wiel et al. (2019).
Sampling extreme events
We use the empirical sampling method to analyse changes in extreme drought (i.e. events of 100-year return period) in response to global warming (Figure 3). A similar analysis based on a GEV-fit to 100 years of simulated data shows almost no statistically significant changes due to the large uncertainties involved.
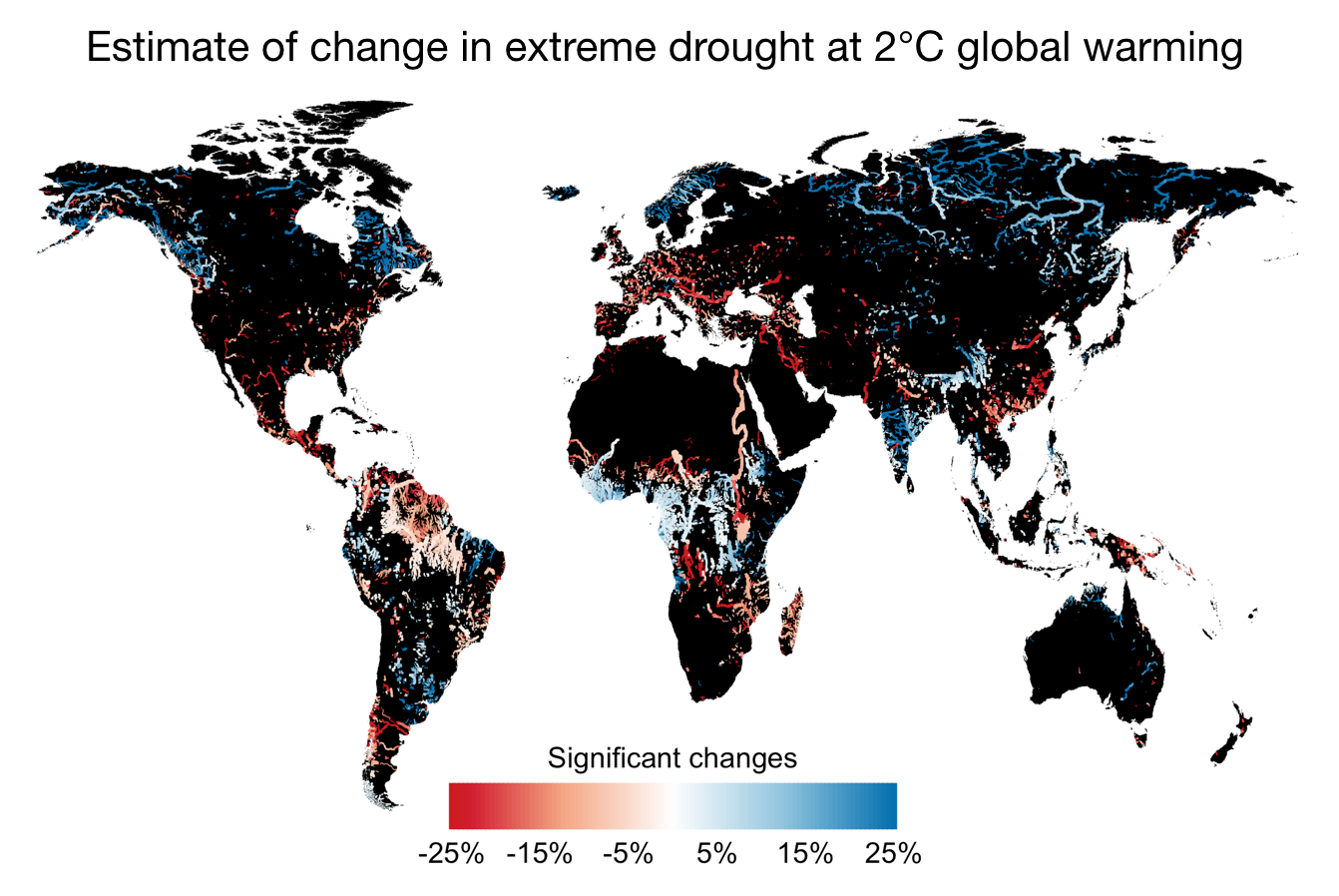
Figure 3: Estimated change in the 1-in-100 year drought based on river discharge. Percentage change between a 2°C-warming scenario and present-day conditions, only statistically significant changes are shown. Figure adapted from Van der Wiel et al. (2019).
It is important to note that our large ensembles were created with a combination of one atmospheric and one hydrological model. Such data can be used to quantify internal variability and extreme events without model-formulation based uncertainty. This is different from multi-model ensembles. Multi-model approaches reduce the impact of model biases, but lead to rapid increases in computational demand. Consequently, a lower number of simulations can be done per model, which has consequences for the investigation of the most extreme events. For example, with 10 models doing a 200 year simulation, one can analyse the 1-in-200 year event and provide an estimate of model-based uncertainty. This is different from having 1 model with 2000 years of simulation, which allows an analysis of the 1-in-2000 year event though without information on model-based uncertainty. Different research projects require different experimental setups; short multi-model experiments are not in all cases preferable over single-model large experiments.
It is our hope that the large ensemble approach will become more common in the future. It can be used to complement analyses using statistical extrapolation or short (multi)model simulations, but will also open new lines of research into the physical processes leading to the most extreme hydrological events.
*Karin van der Wiel is a postdoctoral researcher at the Royal Netherlands Meteorological Institute (KNMI). This study was done in close collaboration with the Department of Physical Geography of Utrecht University.
Full paper
Van der Wiel, K., Wanders, N., Selten, F.M., & Bierkens, M.F.P. (2019): Added value of large ensemble simulations for assessing extreme river discharge in a 2 °C warmer world. Geophysical Research Letters, in press, doi: 10.1029/2019GL081967.
0 comments