How model uncertainty, diagnostics & information theory are interconnected in earth sciences – Interview with Hoshin Gupta

Contributed by Ilias Pechlivanidis. 

Hoshin Gupta’s work is among the most highly cited in the hydrological scientific field, and has received a number of awards and medals, including the 2014 EGU Dalton Medal and 2017 AMS RE Horton Lecture award. Hoshin has for many years been interested in a deeper understanding of models and data to be better used to enhance the learning process of how dynamical environmental systems work. In addition, particularly to many young researchers, Hoshin is well known for the Kling-Gupta Efficiency (KGE; Gupta et al., 2009) metric, which in many modelling applications is now used as a performance evaluation benchmark.

I personally met Hoshin for the first time in 2007, when a scientific question related to my PhD topic eventually led to a 3-hour discussion. It was then that I realized that Hoshin is, in addition, a great mentor to students and colleagues, with an open mind to new ideas and methods.

Back in May of 2018, a workshop on information theory and the earth sciences took place at IHCantabria with Hoshin being among the key drivers to its success. There, I had the opportunity to speak with him about model uncertainty, diagnostic model approaches, and ways that information theory can be used for hypothesis testing, causality and extraction (discard) of information (disinformation).

Ilias Pechlivanidis (IP): Parameter optimization, uncertainty, model diagnostics and now information theory. This journey has taken more than 30 years and you have been a key driver, yet how easy has it been for a community to develop momentum and shift or even evolve the scientific focus?

Hoshin Gupta (HG): You are probably right that perspectives evolve slowly over timescales of decades. I’m not sure why that is, but it seems consistent with the idea that one needs to investigate and practice something for on the order of 10,000 hours to understand it deeply (e.g., to achieve some level of mastery in music, or martial arts, or meditation, etc., so why not in science?). For my part, also I think this time scale has been relevant to me being able to meet many smart young (and not so young) people against whom I could bounce my crazy ideas and interests. So perhaps there is an element also of how rapidly ideas mature in a community. I guess I’ve never been focused on the time aspect of it, just the curiosity to go deeper. It seems that sensible ideas (ones that seem logical and provide tangible benefits to operational use) get recognized and adopted rather quickly, so that is an encouraging thing.

IP: Collection, quality assurance and standardization of data needed in hydrological modelling is an expensive process. Yet different datasets are increasingly becoming available in high spatiotemporal resolution (even over the globe) and near to real time, i.e. earth observations, microwave links, drones etc. Is it really a matter of “lack of” data that we do not have a perfect understanding of system behavior?

HG: Ahhh, you give me an opportunity to jump on my bandwagon!! Leaving aside the issue of whether “perfect understanding” is attainable, it seems clear to me that it is not the amount of “data” that is important, but instead the amount of relevant information contained in that data, and our ability to extract and use it properly. I do think that when data was scarce, people were forced to “milk” the data for all it was worth, at least to the best of their abilities, and many early scientific advances probably reflect this fact. The challenge now seems to be that our ability to process and interpret data (i.e., to extract useful information from it) may not be keeping up with the huge volumes continually being made available. It is possible that we can run into serious problems of even being able to store that data long enough to be able to properly mine it for valuable information. Arguably, evolution developed the method of “modeling” (models we build, first in our brains and then share and develop further through communal processes) as a way of compressing useful information to be used in support of survival. One of the most interesting challenges today is to find efficient and effective ways to combine theoretical knowledge (the results of past information extraction) with the information contained in data becoming available through new data collection technologies. In the past, we tended to average over space and time (lumping) to arrive at relatively “simple” explanations. Perhaps we can now use our increasingly sophisticated computational capabilities and artificial intelligence strategies to develop “better” explanations that actually work at the space-time scales need to obtain robust solutions to human problems.

IP: Information theory (IT) seems to be your newest scientific interest. Although some application of IT in hydrological modelling can be found since 80s, why do you think there is a comeback to IT once again? Does IT provide a way to extract information and enhance knowledge in comparison to “traditional” uncertainty methods?

HG: It is true that IT poked its head into hydrology in the 1970’s before going dormant for some time. My guess is that hydrology as a science has been slowly maturing, parallel with the fact that computational capabilities and data availability have been expanding. For myself, I think I had to become more well versed in concepts of probability theory and Bayesian logic before I was ready to start understanding what IT has to offer. There is now a small, but rapidly growing community of people who are exploring the answer to your question (see http://swites.ihcantabria.com/).

I was first properly introduced to the topic by Gong Wei who helped me to see how IT was relevant to the problem of understanding epistemic uncertainty (model structural error). Since then I have been heavily influenced by my conversations with Grey Nearing, Uwe Ehret, Steven Weijs and Ben Ruddell, beginning with the question of “how to characterize and measure the information content of models” (Shannon and others showed how to do that for data), and the related question of “how to establish whether a given data set contains information not yet assimilated into an existing model” (and of course, what that information is).

I have long been suspicious of the focus on quantifying “uncertainty”, feeling that this focus has been somewhat of a “red herring” (distraction). I am now convinced by Grey’s arguments that rigorous uncertainty quantification is not possible and that, consequently, scientific approaches that depend on doing so can lead to all kinds of questionable conclusions. Instead, Grey has argued for a scientific method rooted in IT as a dual/complement to probability theory, in which the focus is not on whether a model is “correct” or more/less uncertain, but instead on whether a model can be further improved to the point that there is no further useful information contained in a given data set (and therefore the data set can be discarded). Now while, such a model could perhaps be constructed using pure data-mining methods (what might be termed a black-box model), we are preferentially interested in models that remain consistent with known physical laws, principles and other facts, so that the underlying structure and functioning of a system can be better understood (in addition to providing better predictions) and so that questions of the “what-if” kind can be explored.

IP: Communication of uncertainty has always been a challenge to service providers. Nevertheless, users increasingly understand better uncertainty in model outputs and manage to take decision. Information theory provides a glossary focusing on the model outcome driven by the information that is present. Do you believe that a paradigmatic shift on how we communicate uncertain model outputs will result into better decision-making?

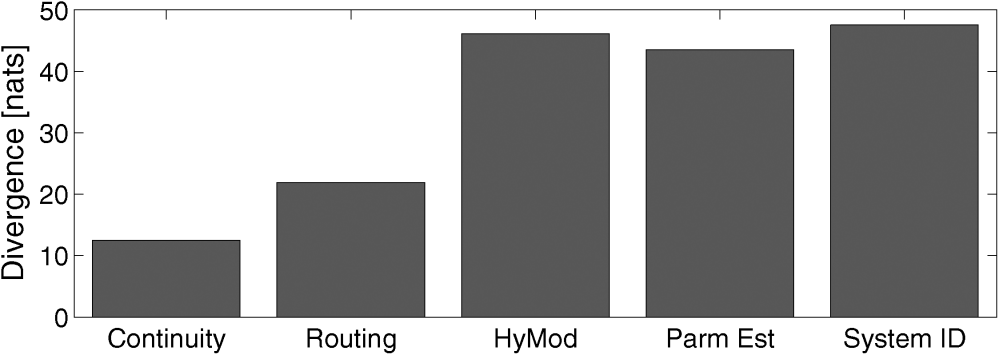
HG: I tend to think that a focus on “uncertainty” associated with a model output can obscure the more important question of what useful “information” a model can provide that is relevant to a decision. While quantifying uncertainty robustly seems impossible, the converse – quantifying information gain (value) – is very possible. This means that, arguably, it is not actually possible to properly quantify the risks associated with a decision (although we can come up with a qualitative understanding of those risks). However, we can quantify the reduction of risk, because this only requires quantification of the information gain (change in uncertainty brought about by some new information).

Similarly, I think that scientists should not speak in terms of how “certain” we are (there is a lot of statistical literature questioning the validity of “confidence intervals”) … instead we should highlight whether or not a given decision reflects the best available information at any given moment. It would be a fool who would refuse to act (make a decision) based on the best available information, even if that decision is to not do anything for the moment. The challenge is to develop methods that properly exploit the available information, and I think that this is where development of IT as an approach to studying the world has the potential to provide a powerful and productive way forward.

Thank you, Hoshin, for this insightful interview. On behalf of all the HEPEX members we will like to thank you for this contribution, and we will be keeping an eye on potential applications of information theory in hydrological forecasting.

References

Gong, W., H. V. Gupta, D. Yang, K. Sricharan, and A. O. Hero III (2013), Estimating epistemic and aleatory uncertainties during hydrologic modeling: An information theoretic approach, Water Resour. Res., 49, doi:10.1002/wrcr.20161.

Gupta, H. V., Kling, H., Yilmaz, K. K., & Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology, 377(1–2), 80–91. https://doi.org/10.1016/j.jhydrol.2009.08.003

Nearing, G. S., and H. V. Gupta (2015), The quantity and quality of information in hydrologic models, Water Resour. Res., 51, 524–538, doi:10.1002/2014WR015895.

Other relevant reading

https://link.springer.com/content/pdf/10.1007%2Fs11707-018-0709-9.pdf

https://export.arxiv.org/pdf/1704.07512

https://www.tandfonline.com/doi/full/10.1080/02626667.2016.1183009